Note to reader
I do not include large code snippets as this was an assignment for my parallel computing course at Northwestern and I don’t want future students copying it. It exists in a private repo of mine containing my school assignments. I will try to do my best to illustrate the work I did with fewer code examples
Github Link
- Private url
Overview
This project parallelizes a contrast stretching algorithm using MPI to enable high-performance image processing on distributed systems. The final implementation achieved approximately a 10× speedup over the sequential baseline.
To get there, I first created a shared-memory version using OpenMP. While this brought notable gains, the most interesting and scalable results came from the MPI-based distributed implementation. Special considerations—like ghost rows, data convergence, and uneven chunk sizes—were handled carefully to ensure both correctness and performance.
What Is Contrast Stretching?
Contrast stretching enhances image clarity by expanding the range of pixel intensity values.
It’s essentially a nearest neighbors operation, where each pixel’s new value depends on its neighboring pixels. In a sequential setting, this simply means iterating over every non-boundary pixel and adjusting its value accordingly.

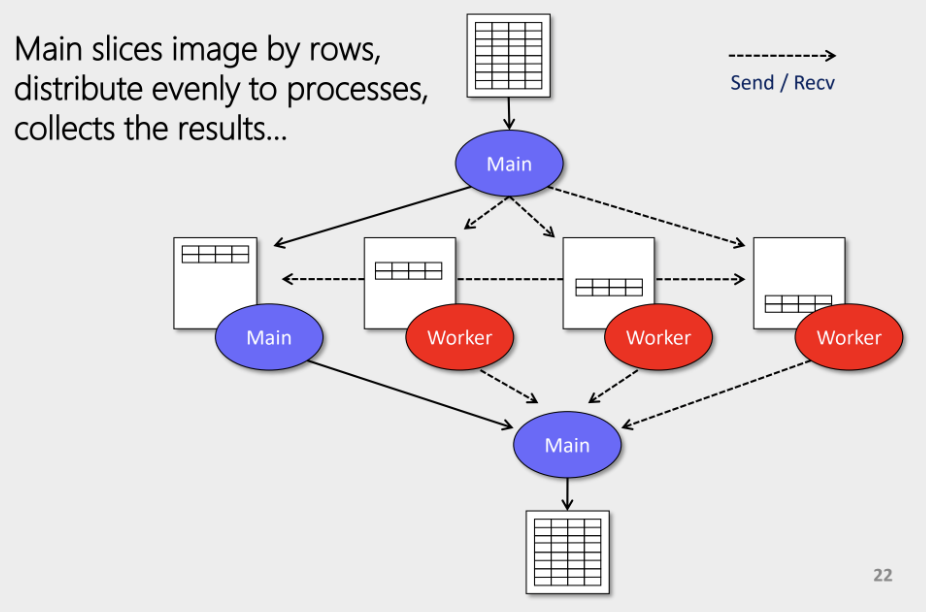
The Sequential vs. Distributed Approach
In a naïve distributed version, each worker could receive the entire image, process its part, and return results. But that would be extremely memory-inefficient.
Instead, a more optimal strategy involves:
- Splitting the image into horizontal chunks (rows).
- Distributing chunks among workers.
- Each worker processes only its assigned chunk.
- Processed chunks are gathered and stitched together.
//
// When it is the main process, we are scattering the image.
//
uchar* sendbuf = (rank == 0) ? image[0] : NULL;
//
// New2dMatrix flattens a matrix into a 1D representation
// This is the recieve buffer. We let the main process handle leftover rows
//
uchar** subset_buf = (rank == 0) ? New2dMatrix<uchar>(leftover_chunk_size + 2, cols * 3) : New2dMatrix<uchar>(chunk_size + 2, cols * 3);
//
// Scattering to each worker based on the size (counts) and offsets (displacements)
//
MPI_Scatterv(
sendbuf, counts, displacements, MPI_UNSIGNED_CHAR,
subset_buf[1], counts[rank], MPI_UNSIGNED_CHAR,
0, MPI_COMM_WORLD
);
This high-level strategy solves the memory issue, but introduces three key technical challenges.
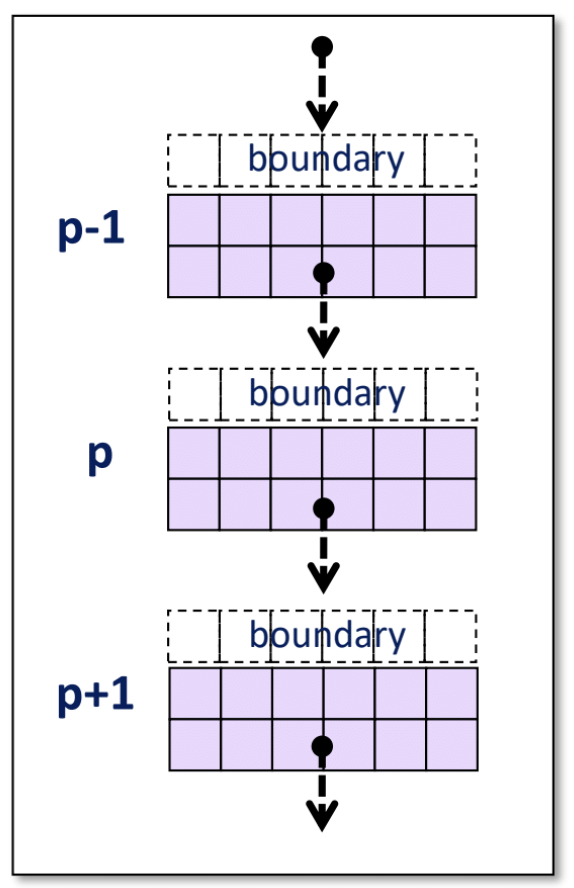
Challenge 1: Ghost Rows (Halo Exchange)
Since contrast stretching depends on neighboring pixels, each worker also needs access to the rows immediately above and below its chunk—even though they belong to another worker.
Example:
- Worker 1 needs:
- The top row from Worker 2.
- The bottom row from Worker 0.
These are known as ghost rows and must be exchanged between adjacent processes before each computation step.
//
// Changing the destination and src based on the current node rank
//
int dest = (rank < numProcs - 1) ? rank + 1 : MPI_PROC_NULL;
int src = (rank > 0) ? rank - 1 : MPI_PROC_NULL;
//
// Halo exchanges
//
MPI_Sendrecv(
image[rows], COLS, MPI_UNSIGNED_CHAR, dest, tag,
image[0], COLS, MPI_UNSIGNED_CHAR, src, tag, MPI_COMM_WORLD,
MPI_STATUS_IGNORE
);
MPI_Sendrecv(
image[1], COLS, MPI_UNSIGNED_CHAR, src, tag,
image[rows+1], COLS, MPI_UNSIGNED_CHAR, dest, tag, MPI_COMM_WORLD,
MPI_STATUS_IGNORE
);
Challenge 2: Alignment and Convergence
In a distributed setting, it’s critical that all processes are working with consistent and up-to-date data. Misaligned ghost rows can cause incorrect results.
To handle this:
- After each processing round, workers exchange ghost rows with neighbors.
- This ensures alignment across all parts of the image.
- Convergence is achieved when no further changes occur across any worker’s chunk.
int step = 1;
bool converged = false;
while (step <= steps && !converged)
{
// Ghost exchange
// Each worker processes their chunk here
// ...
//
// Gathering the number of pixel differences from each worker
//
int global_diffs = 0;
MPI_Reduce(&diffs, &global_diffs, 1, MPI_INT, MPI_SUM, 0, MPI_COMM_WORLD);
MPI_Bcast(&global_diffs, 1, MPI_INT, 0 /* sender */, MPI_COMM_WORLD);
//
// If the number of differences across all workers is 0, then we can stop going through the loop
//
converged = (global_diffs == 0);
}
Challenge 3: Uneven Chunk Sizes
Image dimensions don’t always divide evenly across the number of processes. If the height of the image isn’t divisible by the number of workers, chunk sizes will vary.
To address this:
MPI_Scattervis used to distribute varying chunk sizes.- Each worker handles the correct number of rows, and the final image is reconstructed seamlessly.
//
// This contains the chunk sizes for each worker:
// int counts = { 308, 307, 307, 307, 307 } for n = 5
//
int counts[numProcs];
counts[0] = leftover_chunk_size;
for (int i = 1; i < numProcs; i++) {
counts[i] = chunk_size;
}
//
// This calculates the starting position for each process's chunk
// displacements = {0, 308, 615, 922, 1229};
//
int displacements[numProcs];
displacements[0] = 0;
for (int i = 1; i < numProcs; i++) {
displacements[i] = displacements[i - 1] + counts[i - 1];
}
//
// Scaling based on the three color channels (RGB)
//
for (int i = 0; i < numProcs; i++) {
counts[i] *= cols * 3;
displacements[i] *= cols * 3;
}
Speedup on my local macbook
MPI Distributed Solution (Steps = 75, Nodes = 7)
** Done! Time: 8.855 secs
** Writing bitmap...
** Execution complete.
Sequential Solution (Steps = 75)
** Done! Time: 46.147 secs
** Writing bitmap...
** Execution complete.
Local Speedup = 5.21x
Northwestern’s HPC, Quest, achieved ~10x speedup
Summary
Through careful parallelization of a nearest-neighbor image algorithm, this project demonstrates a scalable and efficient approach to contrast stretching using MPI.
Key outcomes:
- ~10× speedup over the sequential version.
- Handled distributed data dependencies with ghost rows.
- Used
Scattervto handle uneven workload distribution. - Achieved convergence with synchronized communication between processes.
- Utilized Northwestern’s high performance computing cluster, Quest, to achieve even better results.